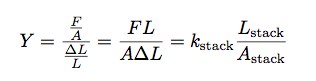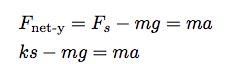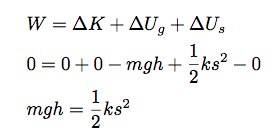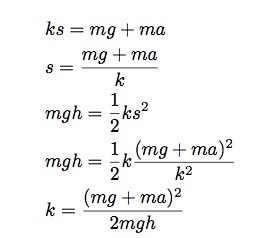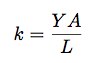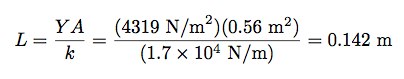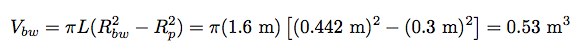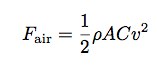编者按:本文仅限于理论探讨。我们绝不建议你轻易尝试。事实上,我们提醒你最好别这么干。
社交新闻网站Reddit上有这样一个问题:你要是想从一楼窗口跳下去并且还能好好活着的话,你需要给自己裹上多少层气泡膜?
谁会问这样的问题?我干嘛要费脑筋回答这样的问题?好吧,这就是我在做的事情,想做就做咯,这就是为什么。或许已经有网友在Reddit网站上回答过这个问题了,但不论如何我还是想亲自实验一探究竟。
在我开始研究这个问题之前,我想把这个问题稍作改动。我确信即使不用气泡膜你也能从一楼窗口跳下去。所以,我猜想问题中所说的“一楼”应该是指二楼的窗口(或者是底楼上面的一层楼)。从这样的高度跳下去其实并不是很难做到。这里是我的跳跃危险系数计算器。(译者注:该计算器指的是本文作者就你到底可以从多高的地方跳下来同时不伤到自己这一问题所做的一系列实验及其结论。详见http://www.wired.com/wiredscience/2009/12/dangerous-jumping-calculator/)跳楼的后果本质上取决于你在着地前下落的高度。
修改之后的问题如下:你需要包裹多少气泡膜才能从6楼窗口跳下去并安然无恙?我们不妨将6层楼这个高度设为20米。
要回答这样一个问题,我们应该从哪里入手呢?好吧,首先我们需要一些气泡膜。我们需要怎样的气泡膜呢?
气泡膜的厚度是多少?
当然,我们有各种类型的气泡膜,不过下图中就是我做实验用的气泡膜。
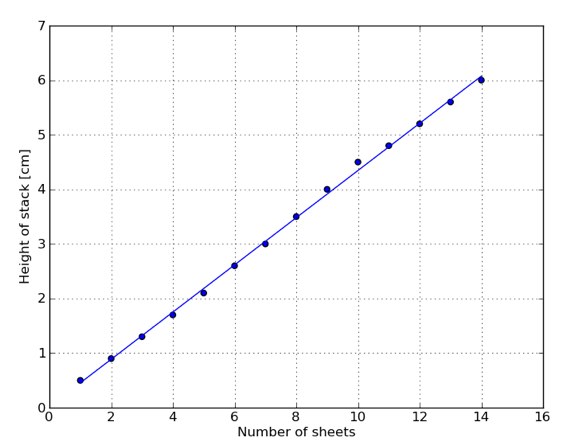
为了让大家更清楚地了解该气泡膜的厚度,我制作了一张格点坐标图。横轴表示纸张数量,纵轴表示相应数量的纸张堆积起来的总厚度(单位:厘米)
如图所示,该线性拟合方程的斜率是0.432厘米/张。因此,我将以这个数据来表示每张气泡膜的厚度。
气泡膜的密度是多少?
我不确定实验是否需要这个数据,但我还是测算了一下。我把气泡膜裁成宽8.8厘米,长14.3厘米的矩形(为什么要这样做呢?很快你就会知道答案了。)通过之前的测算,我们得知该气泡膜的厚度为0.432厘米。于是我们可以算出这样一张矩形气泡膜的体积为54.3立方厘米。为了算出该纸的质量,我增加了纸的层数(每次增加一张)。根据下面的线性拟合图可以算出每张纸的质量。横轴为纸张数量,纵轴为相应数量的纸张的总质量(单位:克)。
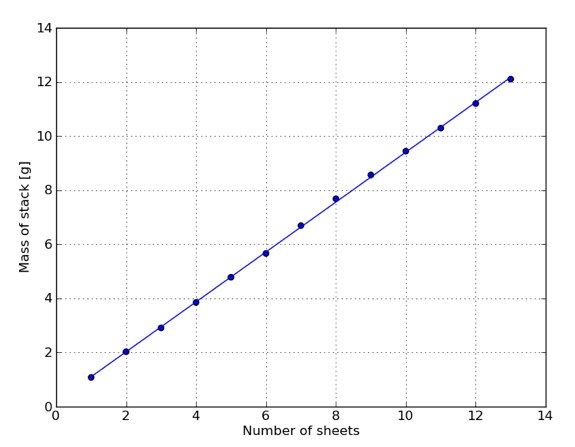
该图所示的线段斜率为0.922克/张,即每张矩形气泡膜的质量约为0.922克。由此,我计算出了该气泡膜的密度为0.017克/立方厘米。考虑到气泡膜(在空气中)具有一定的浮力,因此这并非它真正的密度。不过这也没关系,因为我们总归要把它置于空气中进行实验的。
气泡膜的弹性如何?
当你挤压气泡膜时,它会皱缩。看起来很像弹簧是不是?我不知道。这就是我要做的。我要将14张气泡膜叠起来,然后一边在这叠纸顶上放重物一边测量这叠纸的高度变化。过程如下图所示:
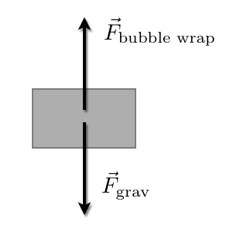
我分析了一下这叠纸上的重物的受力情况,画了以下这张受力分析图:(译者注:向上的箭头代表气泡膜给重物的托力,向下的箭头代表重物的重力。)
因为重物处于静止状态,所以我们可以推断它此时受力平衡,即气泡膜给它的托力与它自身的重力相等。这让我们很容易就能算出气泡膜的弹力。如果说气泡膜确实像弹簧那样的话,那么它施加给重物的力就应该与与其自身的收缩程度成正比。假设我们将气泡膜的收缩程度设为s,那么我们便可得到如下等式:(气泡膜所受到的力等于s与k的乘积。)
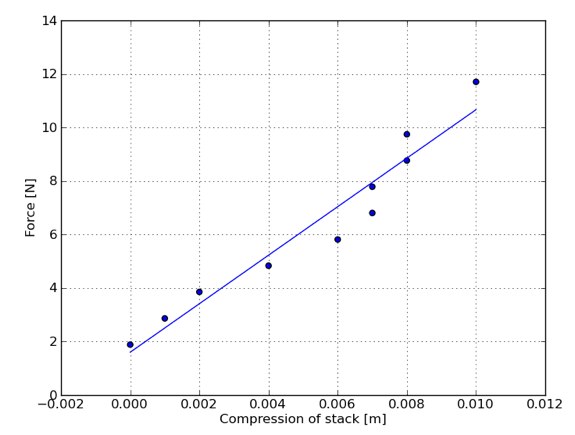
在这个等式中,k为弹性系数,它是一个常量。下图显示了气泡膜受力大小和其收缩程度的关系。(纵轴表示受力大小,单位:牛顿;横轴表示收缩程度,单位:米)
图中线段斜率为906牛顿/米,所以这一叠气泡膜确实存在一个有效的弹性系数。看看这些散点吧,它们几乎分布在同一条写线段上,这说明了气泡膜受力大小和收缩程度确实存在某种线性关系。(太棒了!)
你现在大概在想我可以用这些东西来模拟身体包裹气泡膜进行撞击的实验,对吗?不,还没这么快。如果我把这叠气泡膜增加到原来两倍的厚度会怎样?它还会具有跟之前相同的弹性系数吗?不一定。为什么呢?你可以把每一张气泡膜看作一个弹簧。每一张纸都承载着同样大小的力(前提是我假设每张纸的质量跟重物施予它们的力相比可以忽略不计),所以它们的收缩程度是一样的。如果10张纸的收缩量都是0.1厘米,那么一叠纸的收缩总量就是1厘米(10*0.1厘米)。结论就是纸叠得越厚,有效弹性系数就越低。
此外,如果我选用了一张面积较大的气泡膜,也就相当于有更多弹簧给重物施加了更大的力。如果将纸的面积扩大到原来的两倍,纸堆的收缩总量便缩小到原来的一半。因此,面积越大的气泡膜所具有的有效弹性系数也就越大。现在你大概能够看出我真正需要的其实是气泡膜的杨氏模量而非一张纸的弹性系数。
杨氏模量是用来描述固体材料抵抗形变能力的物理量,它只与物体的材质有关,与物体的大小质量都没有关系。它的计算公式如下:
根据上述公式,我计算出气泡膜的杨氏模量为4319牛顿/平方米。
有了这一数据,不论有多少气泡膜,我们都能够算出它的有效弹性系数。
跳楼
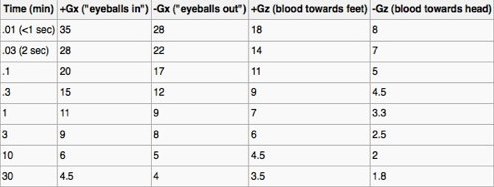
危险的不是跳楼的过程,而是落地的那一刹那。判断落地时安全与否的最佳方法就是计算落地时的加速度。幸运的是,我不用通过实验去搜集人体能够承受的最大加速度的有关数据,因为从美国国家航空航天局那儿就能得到现成资料。以下表格所示的数据就是他们结论的核心部分(请参见百科:http://en.wikipedia.org/wiki/G-force#Human_tolerance)
从上表可知,正常人的身体上能够承受最大加速度的部位是一个可以让“眼球内陷”的部位(译者注:见上表第二列)。也就是说,以该部位着地时,加速度会将眼球“挤”入脑袋。用这条定律来分析跳楼,便能推断出这个部位就是我们的背部。(译者注:跳楼时,人体向下坠落,加速度方向向下。人体背部着地时,虽然身体触地停止运动,但由于存在惯性,加速度方向依然向下,此时,眼球就处于被“挤”入脑袋的状态。)
下面我要正式开始用我的跳跃危险系数计算器来进行这个实验了。不过,还有一个问题。我们在之前所做的计算中规定了自由落体的加速度是一个衡量。如果我们把气泡膜看作弹簧,那么当跳楼者触地停止运动时,加速度也就发生了改变。下面是跳楼者着地瞬间的受力分析图:
关于力和加速度,我们可以写出以下公式(现在我们只要看纵轴方向就可以了):
有上述公式可知,加速度取决于弹性系数和弹簧(即气泡膜)收缩的距离。这两个数据我都不知道。那就让我们用另一个表达式来表示弹簧的收缩距离。假设我把跳楼者、地面和气泡膜(弹簧)看作一个系统。跳楼者在距离地面h的高度起跳,着地时弹簧受到挤压收缩。根据这种情况,我可以写出以下功能定理:
我来解释一下,整个跳楼过程中,跳楼者的速度(由此便产生了动能)在起跳处和着地处都为零。重力势能为mgh(跳楼者质量×重力加速度×起跳高度),弹簧的弹性势能为(1/2)mv2(即(1/2) ×质量×速度的平方)。这样我就有了两个同时含有k和s的表达式。这样就可以把k求出来。
需要声明的是,在上述表达式中,我用a表示跳楼者的最大加速度。此外,我还假设跳楼者完全停下所经过的距离与整个下落距离相比可以忽略不计。不过,即使存在这些小小的出入,这个表达式还是可以立足的。
让我们继续利用这个表达式来求k。我给其中几个变量赋了具体值。
m(质量)=70千克。我假设气泡膜的总质量与跳楼者的体重相比可以忽略不计。等一下我会验证这种假设的科学性。
a(最大加速度)=300米/秒平方 (假设人体与地面的撞击时间不超过1秒钟。这应当是一个合理的假设。)
h(起跳高度)=20米(之前已经提过)
通过这些数据我们可以算出弹簧的弹性系数(k)为1.7 x 104牛顿/米。
需要多少气泡膜?
既然我们现在已经知道了使跳楼者完全停下所需要的弹性系数,毫无疑问我们距离“到底需要包裹多少气泡膜才能安全着陆”这一问题的答案又近了一步。当然,还有一件东西是我们必须首先考虑的——那就是地面与气泡膜接触面的大小。我很清楚,接触面面积会在撞击过程中发生改变——所以我要试着估算出它的具体值。假设该接触面为一个边长为0.75米的正方形。那么,我们就能算出接触面面积为0.56平方米。
:我已经知道了气泡膜的杨氏模量,因此通过以下表达式我可以计算出它的弹性系数:
此处的L是指气泡膜的厚度。L的值可由以下表达式求得:
单张气泡膜的厚度为0.432厘米,因此你需要(14.2厘米)/(0.432厘米/张)=39张气泡膜。这个数字看上去有点小,不过我算出来的就是这么多。、
到底要多少气泡膜?
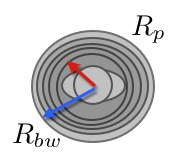
如果我需要包裹39层气泡膜,那这些纸加起来得有多少呢?让我们假设这些纸将跳楼者围起来形成一个圆柱形。详情见下图:
从跳楼者头顶向下俯瞰,裹着气泡膜的人就好比是一个半径为0.3米(这只是个估计值)的圆柱。如果这个圆柱的半径在增加0.142米,那么这些纸的总体积又会是多少呢?好吧,我猜我得找一个身高约1.6米(仍是一个估计值)的人。这样的话,气泡膜的总体积就是:
看来这里确实需要用到气泡膜的密度,多亏我们一早就把它算出来了。由此我们可以算出这些纸的总质量为9千克。这不算太重,但从技术上来说,(由于具体数字的浮动)安全着陆所需的气泡膜的量是会改变的。因此,为了安全起见,我们可能需要多加几层气泡膜。
此外,我们还得考虑以下问题:这个包裹着汽泡纸的跳楼者有多大个头呢?个头的大小会改变这个人下落过程中所受的空气阻力吗?那是当然的。但这种改变足以影响实验结果吗?我会说:非也非也。从仅仅20米高的地方坠落下来,跳楼者几乎不可能达到极限速度。怎么,不相信我么?没关系,其实我也不大相信我自己。要不我们用python编程语言来做一则速算。我会用以下公式来计算空气阻力(就像我通常所做的那样):
上述表达式中,p表示空气密度,A代表圆柱的横截面面积,C代表圆柱的牵引力(阻力)系数。在这种情况下,我假设该圆柱是以柱轴跟地面平行的方式下落的(这样才能使人背部着地)。所以圆柱横截面面积可以表示为L×2R(译者注:L即横截面圆的周长,R为横截面圆的半径。L=2πR,横截面圆的面积=2πR²=L×2R)。我将该圆柱的牵引力(阻力)系数设为1.05。
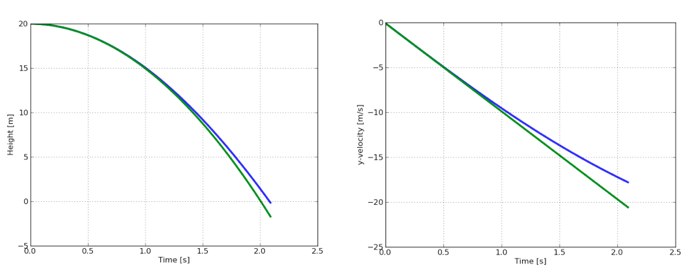
关于数字模型的各种细节我就不多说了,但我们还是有必要看看下面两张图。这两张图显示了在有和没有空气阻力的情况下从20米高处下落的圆柱的高度与时间比(左)及速度与时间比(右)。(译者注:左图纵轴为距离地面的高度,单位:米;横轴为下落时间,单位:秒右图纵轴为下落速度,单位:米/秒;横轴为下落时间,单位:秒)
好吧,我可能出错了。受到空气阻力的圆柱下落时的末速度比较慢(仅为17.8米/秒而非20米/秒)。我得重算么?算了,就当它是一个安全系数吧。
最终答案
我可以裹着39层气泡膜从6楼跳下去。你真会这么做吗?不,别这么干。好吧,我猜你可以拿个假人或者别的什么东西来试一试。
还有一个没法儿用三言两语就能讲明白的问题。你得裹上多少层气泡膜才能从飞机上跳下来而不死。你大概也不需要太多的气泡膜,因为那些纸本身就能减慢你的末速度(译者注:即着地时的极限速度)。
所以说,我还是觉得你不必去摧残那些气泡膜了。还是把它们留着以备不时之需吧。(警告:从窗户跳下去可不是什么好主意——这一点我必须说清楚。)
本文作者赖特·阿兰(Rhett
Allain)是东南路易斯安那大学物理学副教授。他乐衷于物理教学并爱好讨论与物理有关的话题。有时候他把东西拆开却发现无法把它们组装回去。